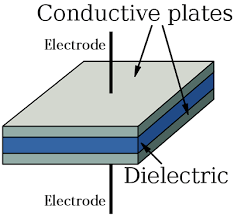
The capacitor contains plates…
The capacitor contains plates…
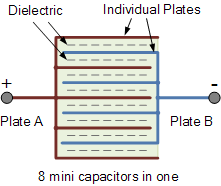
Capacitors
A capacitor stores charge
Questions?
\(Q = CV\)
This is the general definition of capacitance…
\(C = Q/V\)
The charge a capacitor can store, divided by the potential difference applied, is its capacitance.
\(Q = CV\) actually means \(|Q_\text{one plate}| = C \Delta |V_\text{between plates}|\)
Label says 89000 microfarad…
The Van de Graaff generator had much less charge on it. That’s because it has a much smaller capacitance.
Recall: \(\approx 2.48\times 10^{-5}\text{C}\) for \(1.5\times 10^6 \text{V}\).
The capacitor contains plates…




\(\epsilon\) is called the “permittivity”
\(\epsilon_0\) is the “permittivity of free space”
\(\epsilon_0 = \frac{1}{4\pi k}\)
The permittivity of any material is greater than the permittivity of free space, and can be written as
\(\epsilon = \kappa \epsilon_0\)
where \(\kappa\) is the “dielectric constant”
Different materials have a different dielectric constants:
In this class, we will always assume that the field between the two plates of a capacitor is uniform.
Remember, \(\Delta V = -\vec{E} \cdot \Delta \vec{r}\) (for uniform fields)
For parallel plate capacitor, \(\Delta V = \pm E d\)
So, \(C = \frac{Q}{V}\) must go down.
OK, so if I make the plates smaller, the capacitance goes down. That makes sense.
So, \(C = \frac{Q}{V}\) must go up.
So, \(C = \frac{Q}{V}\) must go up.
How much work does it take to charge the capacitor?
Consider a simple parallel-plate capacitor whose plates are given equal and opposite charges and are separated by a distance \(d\). Suppose the plates are pulled apart while the charge on the capacitor remains constant, until they are separated by a distance \(D > d\). What will happen to the potential difference between the plates of the capacitor.
A. it will increase
B. it will decrease
C. it remain the same
Consider a simple parallel-plate capacitor whose plates are given equal and opposite charges and are separated by a distance \(d\). Suppose the plates are pulled apart while the charge on the capacitor remains constant, until they are separated by a distance \(D > d\). What will happen to the energy stored in the capacitor?
A. it will increase
B. it will decrease
C. it remain the same
Consider a simple parallel-plate capacitor whose plates are given equal and opposite charges and are separated by a distance \(d\). Suppose the plates are pulled apart while the potential difference across the capacitor remains constant, until they are separated by a distance \(D > d\). What will happen to the energy stored in the capacitor?
A. it will increase
B. it will decrease
C. it remain the same
Different textbooks use different terms for capacitance of a group of capacitors.
These mean the same thing.
Series: positive to negative
Parallel: positive to positive, negative to negative
What is the potential difference across the capacitors?
Consider the circuit below.
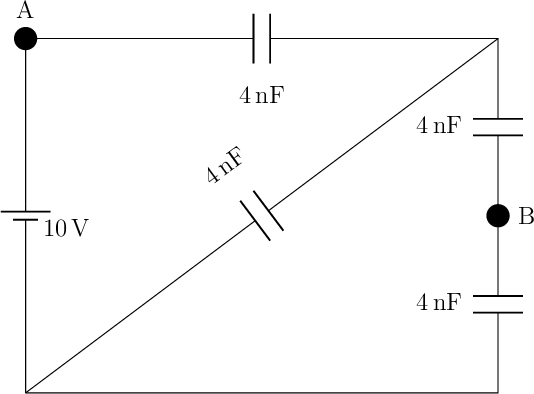
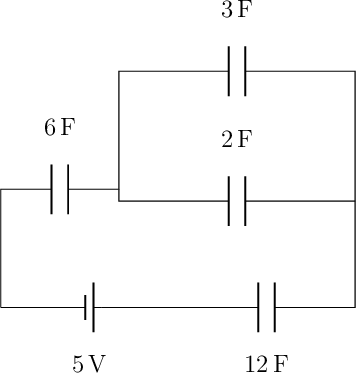
Determine:
\(C_{eff} = \frac{20}{9} \text{F}\)
| 6 F | 3 F | 2 F | 12 F | |
|---|---|---|---|---|
| Q | 100/9 C | 60/9 C | 40/9 C | 100/9 C |
| V | 50/27 V | 60/27 V | 60/27 V | 25/27 V |
Assume that all capacitors are parallel plate capacitors, filled with air, with identical plates. If the voltage of the emf were slowly increased, which capacitor would reach its breakdown limit first?
~
Consider the following experiment:
What will the potential difference between the capacitor terminals be?