Can’t I just use Excel?
Yes, yes you can.
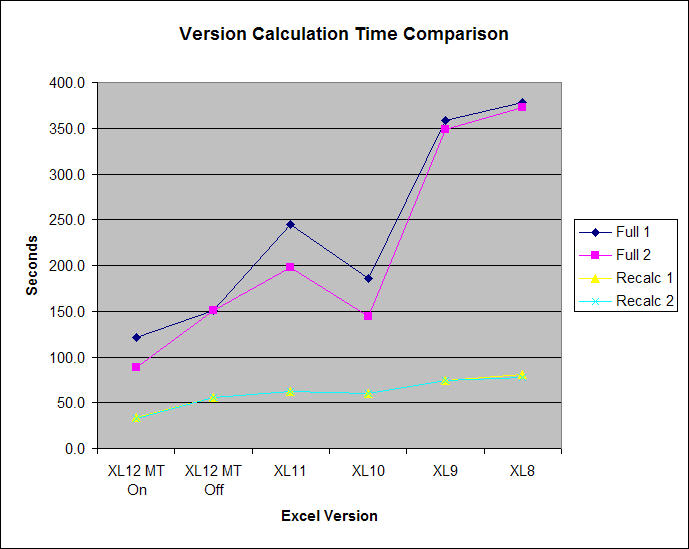
Plotting and Graphical Data Analysis
Yes, yes you can.


This animated gif was created using gnuplot and the
convert command
we can script Gnuplot!!
And:
$ apt search gnuplot
$ apt search gnuplot-x11
...
$ apt install gnuplot-x11
[sudo] password for rshackleford:gnuplot command.plot command will plot data in a filegnuplot> plot 'example.txt'set command is used to configure your plot
set xlabel "text"set ylabel "text"set title "text"./demos/01-intro.sh
plot CommandThe plot command takes 1 or more arguments, which take one or more options
gnuplot> plot 'example.txt', 'multi-column.txt'options:
title : set the text that will appear in the keylinewidth : set the line width usedusing : set the columns that will be plotted
using option.gnuplot> plot 'multi-column.txt' using 1:3with : plot using lines, points, or both
(linespoints)./demos/02-plot_options.sh
x’ for the
independent variable.Functions and Operations:
2*x”sin(x)”exp(x)”x**2”(x + 2)/(x - 2)”You can also define your own functions:
gnuplot> f(x) = 10*x + 2
gnuplot> plot f(x)
gnuplot> g(t) = 2*t - 9.8*t**2 / 2
gnuplot> plot g(x)./demos/03-plotting_functions.sh
Gnuplot reads command from the command line. It can also read commands from a file.
gnuplot> load "plot-data.txt"./demos/04-scripts.sh
png - create PNG image file.jpeg - create JPEG image file.postscript - create postscript image file.x11 - create graph in a windowdumb - create an ASCII image of the graph in the
terminal../demos/05-images.sh
set command.
gnuplot> set xlabel "time (s)"gnuplot> set gridgnuplot> set xrange [0:1]gnuplot> set xtics 0.1gnuplot> help set grid./demos/06-settings.sh
gnuplot> plot 'data.txt' using 1:($2*$2)
gnuplot> plot 'data.txt' using ($1-10):($1*$2)\(P = i^2 R\)
./demos/07-column_transform.sh
gnuplot> m = 2
gnuplot> print m
2
gnuplot> plot m*xgnuplot> plot 'data.txt' with yerrorbars
gnuplot> plot 'data.txt' with xerrorbars
gnuplot> plot 'data.txt' with xyerrorbars./demos/11-error_bars.sh
Note:
1 lbf = 4.448 N
1 m = 3.28 ft
1 hp = 745 W
\(1\;\text{ft}\cdot\text{lbf}\;\times\;1\;\text{rpm} =1\;\frac{\text{ft}\cdot\text{lbf}\;\text{rev}}{\text{min}}\)
\(1\;\frac{\text{ft}\cdot\text{lbf}\;\text{rev}}{\text{min}} \frac{2\pi\;\text{rad}}{\text{rev}} \frac{4.448\;\text{N}}{\text{lbf}} \frac{\text{m}}{3.28 \text{ft}} \frac{\text{min}}{60\;\text{s}} \frac{\text{hp}}{745\;\text{W}} = 0.00019 \; \text{hp} = \frac{1}{5252} \text{hp}\)