More Gnuplot
Fitting functions to data
Part 1: Fitting
- Function fitting is the process of finding a function that passes
through some data.
- Usually, we have an idea of the function that we expect to describe
the data.
Fitting Functions to Data
- Gnuplot can fit arbitrary functions to data with the
fit command.
- The
fit command has the following form
fit <function> "<datafile>" via <parameters>
gnuplot> fit m*x + b 'data.txt' via m,b
Demo : Simple fits
./demos/01-linear_fit.sh
Part 2: Fitting with uncertainty
Recall
- We can plot data with error bars
- We can specify error bars for the \(y\) direction, \(x\) direction, or both.
gnuplot> plot 'data.txt' u 1:2:4 with yerrorbars
gnuplot> plot 'data.txt' u 1:2:3 with xerrorbars
gnuplot> plot 'data.txt' u 1:2:3:4 with xyerrorbars
We can also tell Gnuplot to consider error bars when fitting
Fitting Functions to Data with Errors
gnuplot> fit m*x + b 'data.txt' using 1:2:4 yerrors via m,b
gnuplot> fit m*x + b 'data.txt' using 1:2:3:4 xyerrors via m,b
Demo : Error bars
./demos/02-dataerror_fit.sh
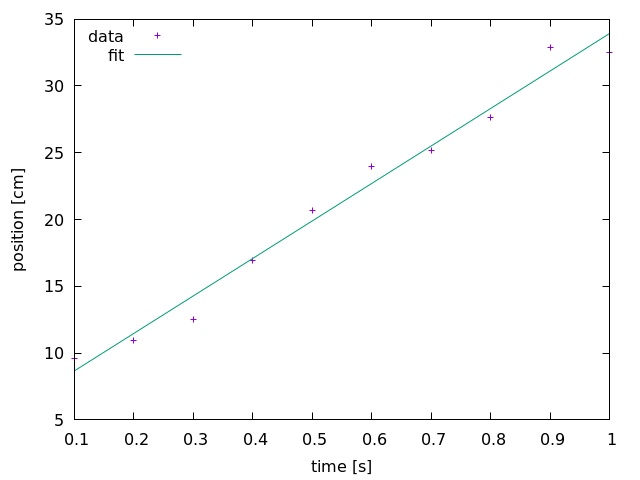
Practice
- The Sandbox directory contains a directory named
fitting.
- The file named
example2.txt contains some data.
- Assume that this data represent the position of a remote control
car, as a function of time, with time measured in seconds and distance
measured in centimeter.
- How fast was the car traveling, on average?
- What is the uncertainty in the car’s speed?
- Where was the car when the timer was started?
- How long would it take the car to travel 1 meter?
- Assume that the third column in the file is an uncertainty for the
car’s position. How does this change the measured speed?
Gaussian Fit
- Gaussian functions show up all over the place
\[N(x,\mu,\sigma) = A e^{-\frac{1}{2}
\frac{(x-\mu)^2}{\sigma^2}}\]
ERROR: could not create image
Example
./demos/03-gaussian_fit.sh
Fitting difficult functions
- Sometimes Gnuplot needs a little help finding the correct fit
parameters.
- Internally, Gnuplot is using an iterative process.
- Try some values
- Compute the sum of deviations squared
- Make a change
- Does it get better?
- If the fit parameters are not already defined as variables, Gnuplot
creates them and gives them initial values (sets them to zero
maybe?)
- If the fit parameters are defined variables, then Gnuplot uses their
current values as the starting point.
Harmonic Oscillator
Recall that, for a mass osccilating on a spring, we have
\[y(t) = A\sin(\omega t)\] \[v(t) = \frac{dy}{dt} = A\omega\cos(\omega
t)\] \[a(t) = \frac{dy}{dt} =
-A\omega^2\sin(\omega t)\] \[T =
\frac{1}{f} = \frac{2\pi}{\omega}\] \[\omega = \sqrt{\frac{k}{m}} \rightarrow k =
(m\omega)^2\]
./demos/05-fitting_difficult_functions.sh
2D plots
Gnuplot can plot functions of two variables as well.
ERROR: could not create image
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Last Slide
Example 2: Kinematics
Say we have collected data for an experiment in Physics I, we
recorded the position of a cart under constant acceleration.
- What is the initial velocity of the cart?
- What is the acceleration of the cart?
- At what time does the cart turn around?
- How far does the card travel before it turns around?
- Is the cart moving faster at the beginning or the end of the data
collection period?
Example 2: Kinematics

- If we fit our data to the kinematics equation, we can:
- “measure” \(x_0\), \(v_0\), and \(a\).
- Use the fit equation to compute other characteristics.
Example 2: Kinematics
What is the initial
velocity of the cart?
. . .

Example 2: Kinematics
What is the acceleration
of the cart?
. . .

Example 2: Kinematics
At what time does the
cart turn around?
. . .

Example 2: Kinematics
How far
does the cart travel before it turns around?
. . .

Example 2: Kinematics
Is
the cart moving faster at the beginning or the end of the data
collection period?
Example 3: Harmonic Oscillator Measurement
Say we have collected data for an experiment in Physics I, we
recorded the position of a mass on a spring while it oscillates and
eventually comes to rest.
Example 3: Harmonic Oscillator Measurement

Example 3: Harmonic Oscillator Measurement

Example 3: Harmonic Oscillator Measurement

Example 3: Harmonic Oscillator Measurement
What is the
maximum displacement of the mass?
. . .

Example 3: Harmonic Oscillator Measurement
What is the maximum speed
of the mass?
. . .

Example 3: Harmonic Oscillator Measurement
If
the mass is 1 kg, what is the spring constant of the spring?
. . .

Example 3: Harmonic Oscillator Measurement
What is the period of
oscillation?
. . .
















