Electric Flux
Gauss’s Law is a law about the electric flux
\[ \Phi = \oint_S \vec{E} \cdot d\vec{A} = \frac{q_\text{enc}}{\epsilon_0}\]
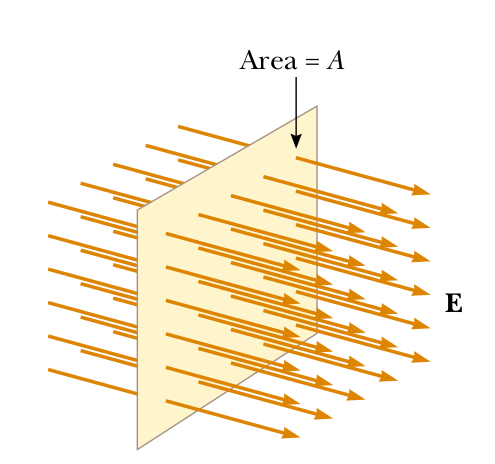
Conceptually, electric flux is proportional to the number of field lines that pass through a surface.
Gauss’s Law
\[ \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_0} \] \[ \nabla \cdot \vec{B} = 0 \] \[ \nabla \times \vec{E} = -\frac{\partial\vec{B}}{\partial t} \] \[ \nabla \times \vec{B} = \mu_0 \vec{J} -\mu_0 \epsilon_0 \frac{\partial\vec{E}}{\partial t} \]
| Differential Form | Integral Form |
|---|---|
| \[ \nabla \cdot \vec{E} = \frac{\rho}{\epsilon_0} \] | \[ \oint_S \vec{E} \cdot d\vec{A} = \frac{q_\text{enc}}{\epsilon_0}\] |
| \[ \nabla \cdot \vec{B} = 0 \] | \[ \oint \vec{B} \cdot d\vec{A} = 0\] |
| \[ \nabla \times \vec{E} = -\frac{\partial\vec{B}}{\partial t} \] | \[ \oint \vec{E} \cdot d \vec{l} = - \frac{d}{dt} \int_S \vec{B}\cdot d\vec{A}\] |
| \[ \nabla \times \vec{B} = \mu_0 \vec{J} -\mu_0 \epsilon_0 \frac{\partial\vec{E}}{\partial t} \] | \[ \oint \vec{B} \cdot d \vec{l} = \mu_0 \int_S \vec{J}\cdot d \vec{l} - \mu_0\epsilon_0\frac{d}{dt} \int_S \vec{E}\cdot d\vec{A}\] |
\[ \oint_S \vec{E} \cdot d\vec{A} = \frac{q_\text{enc}}{\epsilon_0}\]
The net electric flux through a closed surface is equal to the charge enclosed by the surface.
Gauss’s Law is a law about the electric flux
\[ \Phi = \oint_S \vec{E} \cdot d\vec{A} = \frac{q_\text{enc}}{\epsilon_0}\]

Conceptually, electric flux is proportional to the number of field lines that pass through a surface.
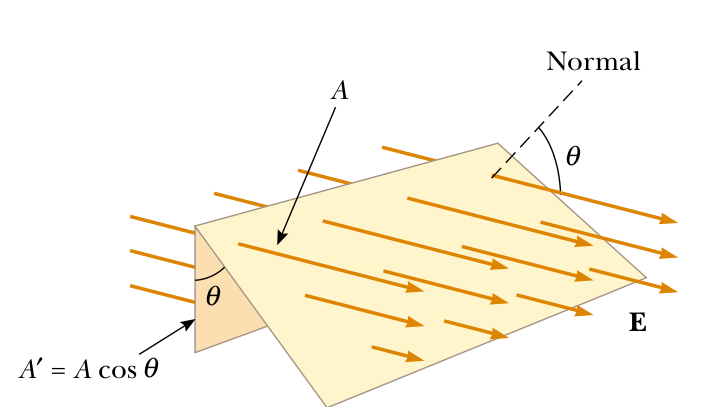
For a uniform field, the flux will be constant over a flat surface, and the integral will just be:
\[ \Phi = \oint_S \vec{E} \cdot d\vec{A}= \vec{E} \cdot \vec{A}\]
where \(\vec{A}\) is an area vector.

For a uniform field, the flux will be constant over a flat surface, and the integral will just be:
\[ \Phi = \oint_S \vec{E} \cdot d\vec{A} = \vec{E} \cdot \vec{A}\]
where \(\vec{A}\) is an area vector.
For a non-uniform field, or an arbitrary surface, the integral calculates the flux by breaking the surface into small area elements, computing the flux for each element, and adding them all together.
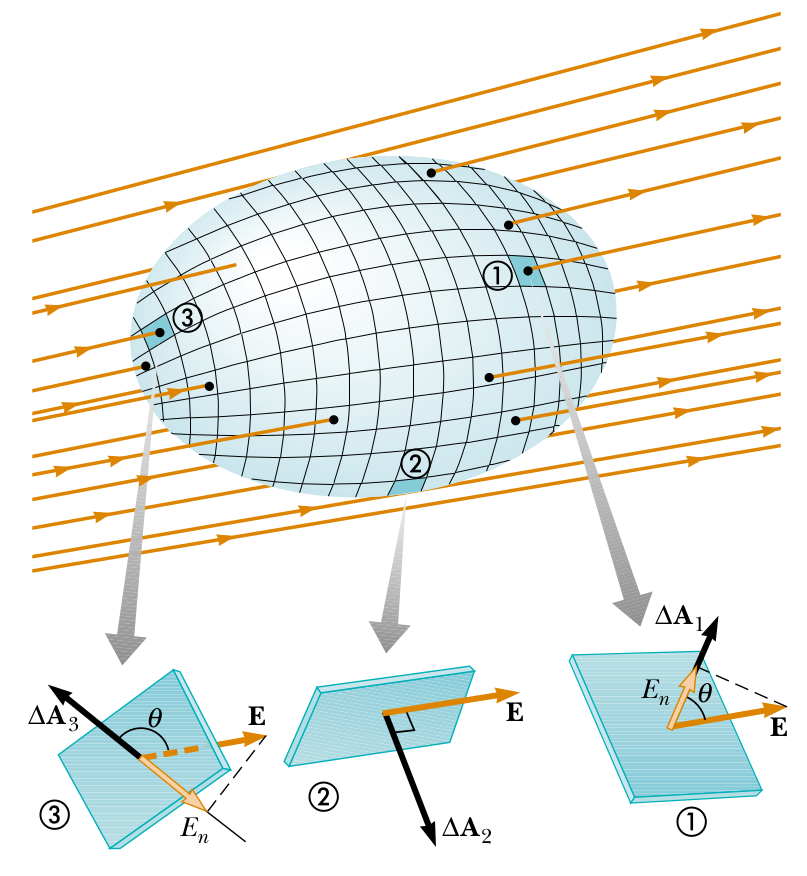
\[ \Phi = \oint_S \vec{E} \cdot d\vec{A} \]
Gauss’s Law gives us Coulomb’s Law!
\[ \oint_S \vec{E} \cdot d\vec{A} = \frac{q_\text{enc}}{\epsilon_0}\]
The electric field inside a conductor must be zero when the conductor is in electrostatic equilibrium.
And Gauss’s Law holds for any imaginary surface…
\[ \Phi = \oint_S \vec{E} \cdot d\vec{A} = \frac{q_\text{enc}}{\epsilon_0}\]
A solid conducting sphere of radius \(a\) carries a net positive charge \(2Q\). A conducting spherical shell of inner radius \(b\) and outer radius \(c\) is concentric with the solid sphere and carries a net charge \(-Q\). Find the electric field in teh regions labeled 1 - 4, and the charge distribution on the shell when the entire system is in electrostatic equilibrium.
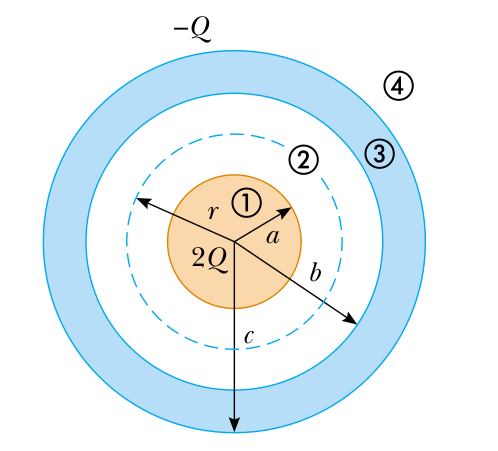

Electric Field produced by:
The dielectric strength of air is \(3\times 10^6\) N/C. This means that for a strong enough electric field (\(> 3\times 10^6\) N/C), air will become a conductor.
How much charge has to build up on the generator for the electric field to exceed the dialectric strength of air?
A sphere of radius \(R\), centered on the origin, has a total charge \(Q\) distributed uniformly through its volume.
Determine the electric field produced by this charge distribution along the \(x\) axis (i.e. what is \(\vec{E}(x,0,0)\)).
Sketch a graph of the x-component of the electric field along the \(x\) axis from \(+\infty\) to \(-\infty\).